Bivariate Significance Tests and Correlation

For this lab, we will be using the transportation.dta dataset created in our previous lab.

Let’s set up our code and open the dataset:

. * Set your working directory to the location of transportation.dta using cd
. use transportation.dta, clear

. describe

Contains data from transportation.dta
Observations:         3,220                  
Variables:            12                  4 Nov 2022 14:25
--------------------------------------------------------------------------------------------------------------------------------
Variable      Storage   Display    Value
name         type    format    label      Variable label
--------------------------------------------------------------------------------------------------------------------------------
geo_id          str14   %14s                  GEO_ID
medianfamilyinc long    %10.0g                S1903_C03_015E
totalworkers    long    %10.0g                S0802_C01_001E
mediantravel    double  %10.0g                S0802_C01_090E
drovealone      long    %10.0g                S0802_C02_001E
mg_county       byte    %23.0g     _merge     Matching result from merge
fips            byte    %10.0g                
state           str14   %14s                  
stateid         byte    %8.0g                 
stateabv        str2    %9s                   
gastax          float   %9.0g                 
mg_gas          byte    %23.0g     _merge     Matching result from merge
--------------------------------------------------------------------------------------------------------------------------------
Sorted by:

First, let’s create a new variable that equals the proportion of workers in the county who drive to work alone.

. gen prop_drovealone = drovealone / totalworkers
(1 missing value generated)

Difference of means and proportions

ttest

The ttest command conducts difference of means test significance tests. In order to compare the means, we need to recode our independent variable into only two groups. Let’s recode the interval variable totalworkers as a measure of the population size of a county into a four-point ordinal measure.

After the recode, we can run the ttest command to see if the mean of prop_drovealone in the smallest counties differs significantly from the mean in the largest counties.

. *difference of means test: 
. recode totalworkers (0/50000=0 "Small")(50000/150000=1 "Med") ///
>     (150000/500000=2 "Large") ///
>     (500000/10000000=3 "Very Large"), gen(size)
(3219 differences between totalworkers and size)

. 
. ttest prop_drovealone if size==0 | size==3, by(size) unequal

Two-sample t test with unequal variances
------------------------------------------------------------------------------
Group |     Obs        Mean    Std. err.   Std. dev.   [95% conf. interval]
---------+--------------------------------------------------------------------
Small |   2,660     .798814    .0014573    .0751583    .7959566    .8016715
Very Lar |      44    .6875035    .0275601    .1828133    .6319232    .7430838
---------+--------------------------------------------------------------------
Combined |   2,704    .7970028    .0015248    .0792899    .7940129    .7999927
---------+--------------------------------------------------------------------
diff |            .1113105    .0275986                .0556615    .1669595
------------------------------------------------------------------------------
diff = mean(Small) - mean(Very Lar)                           t =   4.0332
H0: diff = 0                     Satterthwaite's degrees of freedom =  43.2408

Ha: diff < 0                 Ha: diff != 0                 Ha: diff > 0
Pr(T < t) = 0.9999         Pr(|T| > |t|) = 0.0002          Pr(T > t) = 0.0001

This table is a little confusing! Let’s focus on what matters. In the “Mean” column, you can see the ${y_1}$ and ${y_2}$ . The “diff” row shows ${y_1} - {y_2}$ , the standard error of the difference, and the 95% confidence interal around the difference. The two-tailed p-value is available underneath “Ha: diff!= 0”.

prtest

Difference of sample proportions significance tests can be conducted using the command prtest. The syntax follows ttest. In order to run the command, you need to have a dummy variable for your dependent variable. Notice the use of Z scores instead of t scores below.

. *difference of proportions test:
. recode mediantravel (0 /20=1 "Short")(20/100=0 "Long"), gen(shortcommute)
(1483 differences between mediantravel and shortcommute)

. 
. prtest shortcommute if size==0 | size==1, by(size)

Two-sample test of proportions                 Small: Number of obs =     1154
Med: Number of obs =      149
------------------------------------------------------------------------------
Group |       Mean   Std. err.      z    P>|z|     [95% conf. interval]
-------------+----------------------------------------------------------------
Small |   .3214905   .0137486                      .2945437    .3484373
Med |   .1610738   .0301149                      .1020497    .2200979
-------------+----------------------------------------------------------------
diff |   .1604166   .0331048                      .0955323     .225301
|  under H0:   .0400104     4.01   0.000
------------------------------------------------------------------------------
diff = prop(Small) - prop(Med)                            z =   4.0094
H0: diff = 0

Ha: diff < 0                 Ha: diff != 0                 Ha: diff > 0
Pr(Z < z) = 1.0000         Pr(|Z| > |z|) = 0.0001          Pr(Z > z) = 0.0000

$^2$ test

Chi-squared tests can be conducted very easily using the crosstab syntax. Just add the chi2 option at the end of your command. Stata will print the value of $^2$ , the degrees of freedom of the test, and the p-value below the crosstab.

. tab shortcommute size, col chi2

+-------------------+
| Key               |
|-------------------|
|     frequency     |
| column percentage |
+-------------------+

RECODE of |
mediantrav |
el |
(S0802_C01 |   RECODE of totalworkers (S0802_C01_001E)
_090E) |     Small        Med      Large  Very Larg |     Total
-----------+--------------------------------------------+----------
Long |       783        125        132         44 |     1,084 
|     67.85      83.89      97.06     100.00 |     73.10 
-----------+--------------------------------------------+----------
Short |       371         24          4          0 |       399 
|     32.15      16.11       2.94       0.00 |     26.90 
-----------+--------------------------------------------+----------
Total |     1,154        149        136         44 |     1,483 
|    100.00     100.00     100.00     100.00 |    100.00 

Pearson chi2(3) =  80.8787   Pr = 0.000

Pearson’s r

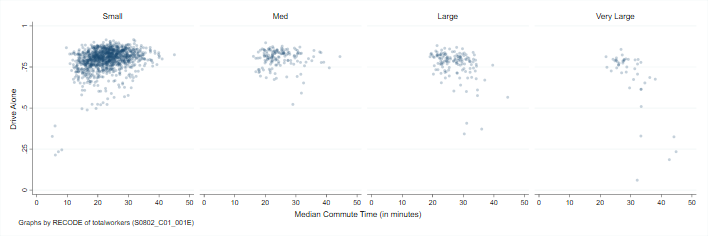
As you know, Persons’s r correlation coefficient is appropriate for continuous/interval data. Let’s take a quick look at a scatterplot first, then we can play around with running correlations on these variables.

. scatter prop_drovealone mediantravel, by(size, rows(1) graphregion(color(white)) ///
>     plotregion(color(white)) ) subtitle(, bcolor(white) lwidth(none)) ///
>     mcolor(navy%25) msize(small) mlwidth(none) ///
>      ysize(2) xsize(6) xtitle("Median Commute Time (in minutes)") ///
>     xlabel(0(10)50) ylabel(0(.25)1) ///
>     ytitle(Drive Alone)

To run a correlation, I recommend using Stata’s pwcorr command. The syntax is very simple: just list the variables you want included in a correlation matrix after pwcorr. You can request a p-value by including the sig option or you can star all correlations that are significant at specific significance levels by using the star() option.

. pwcorr mediantravel prop_drovealone

| median~l prop_d~e
-------------+------------------
mediantravel |   1.0000 
prop_drove~e |   0.0581   1.0000 

. pwcorr mediantravel prop_drovealone, sig

| median~l prop_d~e
-------------+------------------
mediantravel |   1.0000 
|
|
prop_drove~e |   0.0581   1.0000 
|   0.0253
|

. pwcorr mediantravel prop_drovealone, star(.05)

| median~l prop_d~e
-------------+------------------
mediantravel |   1.0000 
prop_drove~e |   0.0581*  1.0000

To control for a third variable, use the bysort prefix. bysort can be specified in front of many Stata commands to run the command by categories of the variable(s) listed. In the case of the example below, we can calculate the correlation between prop_drovealone and mediantravel inside of each size category:

. bysort size: pwcorr prop_drovealone mediantravel, star(.05)

--------------------------------------------------------------------------------------------------------------------------------
-> size = Small

| prop_d~e median~l
-------------+------------------
prop_drove~e |   1.0000 
mediantravel |   0.2891*  1.0000 

--------------------------------------------------------------------------------------------------------------------------------
-> size = Med

| prop_d~e median~l
-------------+------------------
prop_drove~e |   1.0000 
mediantravel |  -0.0344   1.0000 

--------------------------------------------------------------------------------------------------------------------------------
-> size = Large

| prop_d~e median~l
-------------+------------------
prop_drove~e |   1.0000 
mediantravel |  -0.3848*  1.0000 

--------------------------------------------------------------------------------------------------------------------------------
-> size = Very Large

| prop_d~e median~l
-------------+------------------
prop_drove~e |   1.0000 
mediantravel |  -0.7063*  1.0000 

--------------------------------------------------------------------------------------------------------------------------------
-> size = .
no observations

Finally, it is nice to look at multiple bivariate correlations in the same correlation matrix. The matrix below does not control for gastax; instead, it shows the bivariate correlation between mediantravel and gastax (.1809) and between gastax and prop_drovealone (-.0033).